Optimisation of the neighbour rank

The intra-molecular atom distances are a critical feature of the molecules used by ML-LPA to analyse and then predict the lipid phases. However, this feature is based on the given neighbour rank, for which the optimal value has to be determined by the user. This tutorial demonstrates how ML-LPA can be used to easily find the optimal neighbour rank.

Definition of the neighbour rank

The neighbour rank in ML-LPA is defined as the relative position of an atom B from a reference atom B along a chain in the molecule.

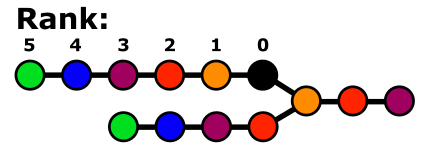
Illustration of the neighbour ranks


In other terms, a pair formed by two atoms at the rank N are (i) on a common chain within the same molecule, and (ii) separated by N-1 atoms along that same chain.

The neighbour rank is essential to define the pairs on which the distances between atoms should be calculated in a molecule. If the rank is too small, the variations in distances might not be significant enough. If the rank is too large, the statistics collected could be insufficient as not enough atoms can form pair at the given rank.

Finding the optimal rank

In order to find the optimal neighbour rank, we will train ML-LPA on the same simulation files, but we will apply different ranks each time and see how the training score is impacted. To avoid extracting the information from the file each time, we will instead use the method .getDistances() of the System class to only compute again the distances at each iteration of the loop.

In this example, we will test all the neighbour ranks from 2 to 10. We will also need to import the NumPy library to analyse the data.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

import mllpa
import numpy as np

# Load the simulations files to be trained on
gel_system = mllpa.openSystem('gel.gro', 'gel.tpr', 'DPPC')
fluid_system = mllpa.openSystem('fluid.gro', 'fluid.tpr', 'DPPC')

# Start the processing loop
all_ranks = np.arange(2,11)
all_scores = []
for rank in all_ranks:

  # Re-generate the distances based on the new rank value
  gel_system.getDistances(rank=rank)
  fluid_system.getDistances(rank=rank)

  # Train the model on the systems - save the model files
  models = mllpa.generateModel([gel_system, fluid_system], phases=['gel', 'fluid'], save_model=True, file_path='dppc_rank='+str(rank)+'.lpm')

  # Get the final total score with the given rank
  all_scores.append( models['scores']['final']['total'] )

# Convert the score list into an array
all_scores = np.array(all_scores)

# Determine the optimal rank by searching the index of the highest score
best_rank = all_ranks[ np.argmax(all_scores) ]
print('Optimal rank:', best_rank)

The optimal rank should be automatically displayed when the script above is run.

For indication, we have found an optimal rank equals to 6 with DPPC simulated with Charmm36 and 4 with DPPC simulated in Martini. This is of course based on our training on our own simulations, and should not be used as a rule.

The maximum rank that can be applied to the system depends on the forcefield model used in the simulation file. For example, an all-atom model such as Charmm36 can have ranks > 20, while coarse-grain models (e.g. Martini) won’t even have any pair at rank 10 or above.

What is next?

Check the API

The following elements have been used in this tutorial: